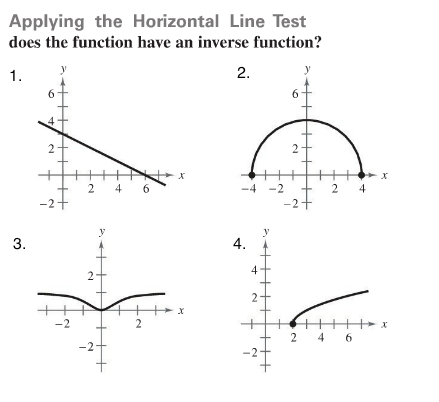
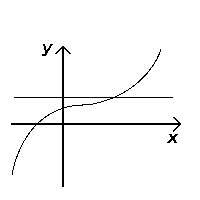Horizontal Line Test

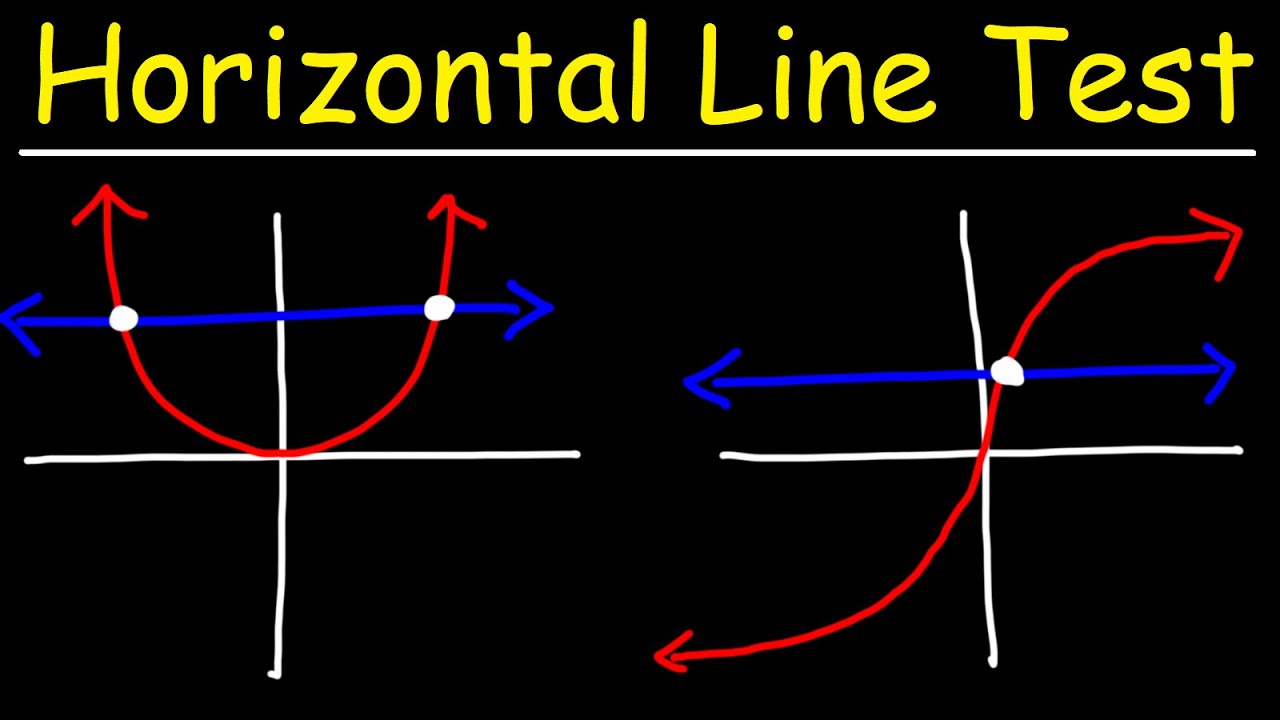
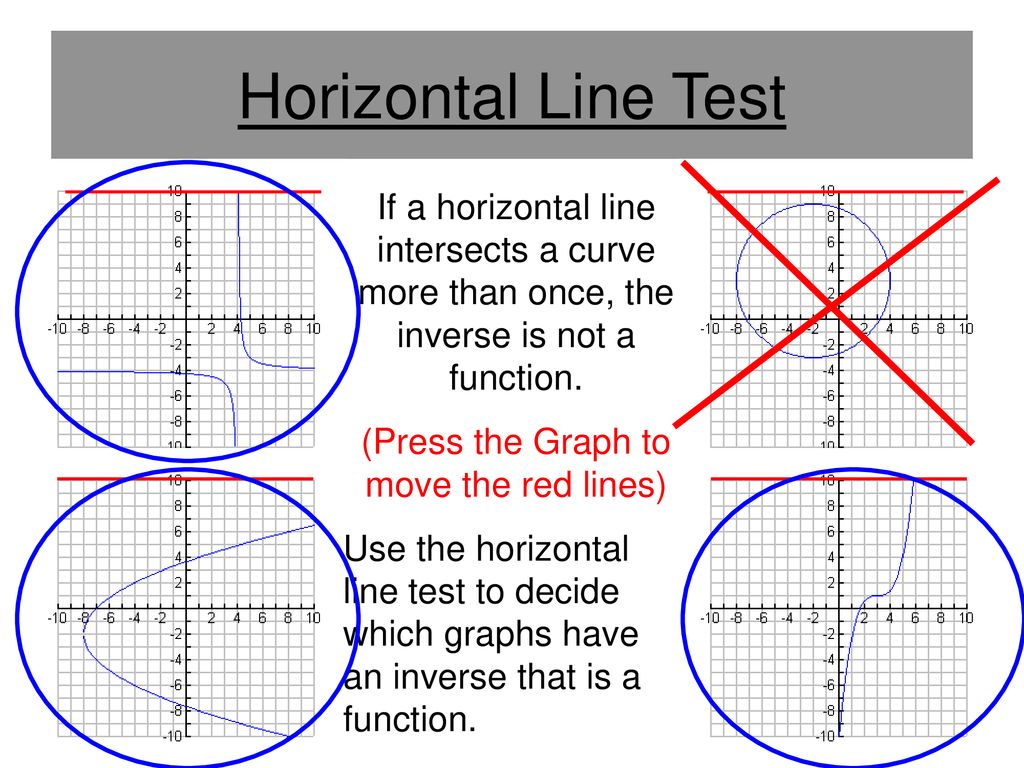
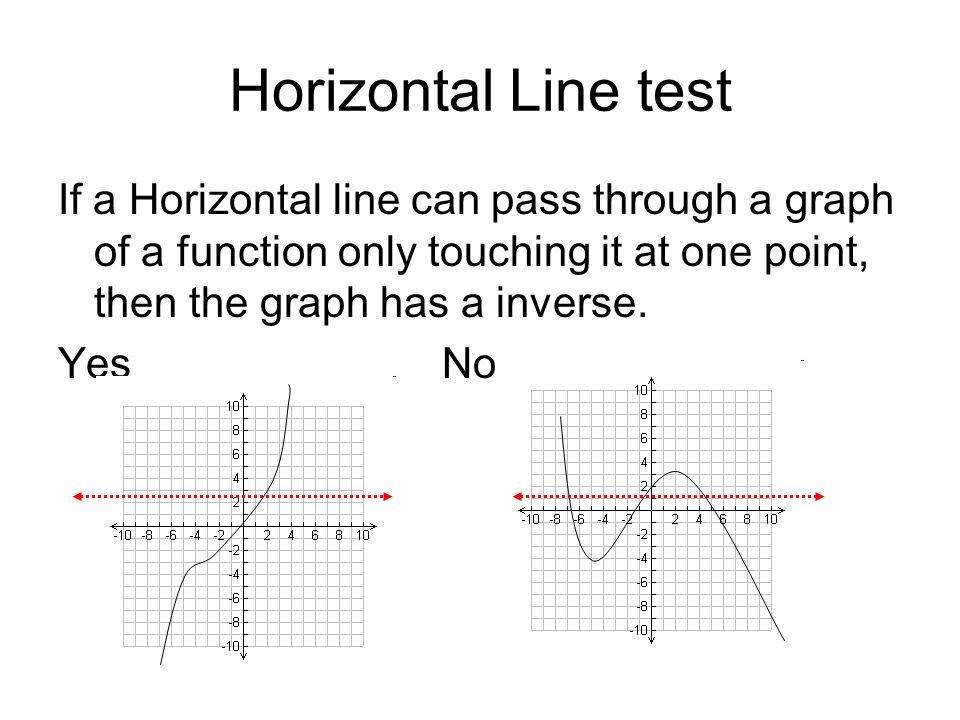
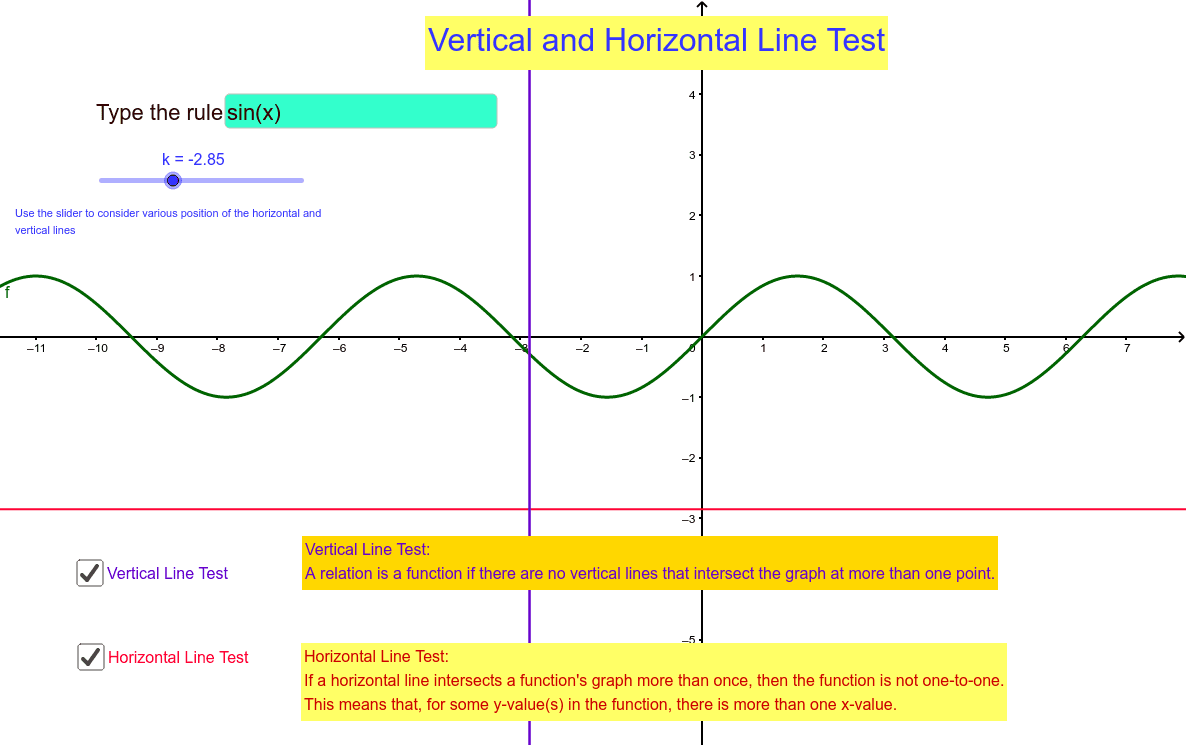
With this test you can see if any horizontal line drawn through the graph cuts through the function more than one time.

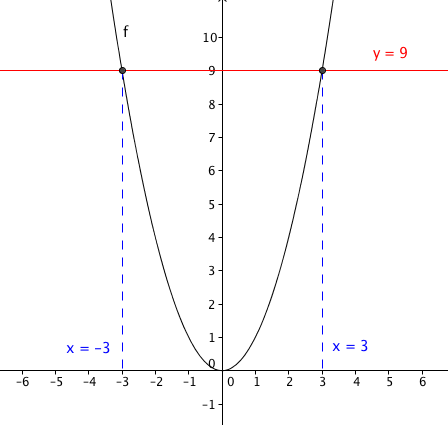
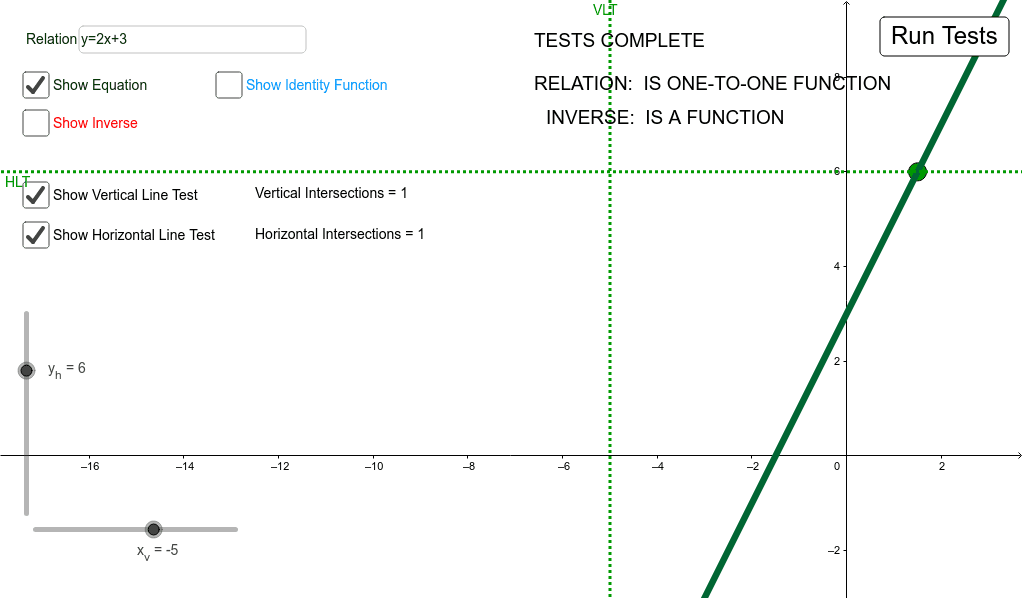
Horizontal line test. The function f is surjective i e onto if and only if its graph intersects any horizontal line at least once. Definition examples horizontal line test. That is if every horizontal line intersects the function at most once then the function has an inverse. X 1.

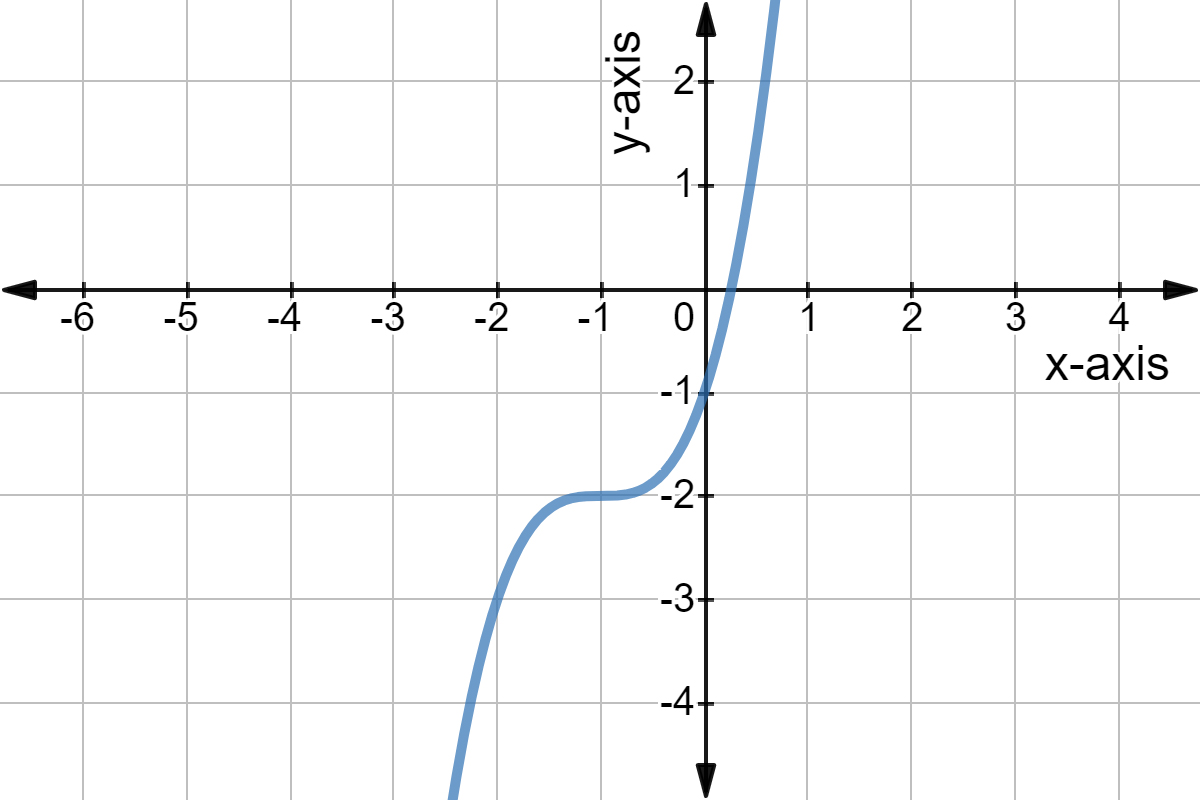
Y x 2 3. The horizontal line test is a method to determine if a function is a one to one function or not. From the discussion above we can conclude that we can use horizontal lines to test whether a function has an inverse or none. This is known as the horizontal line test.

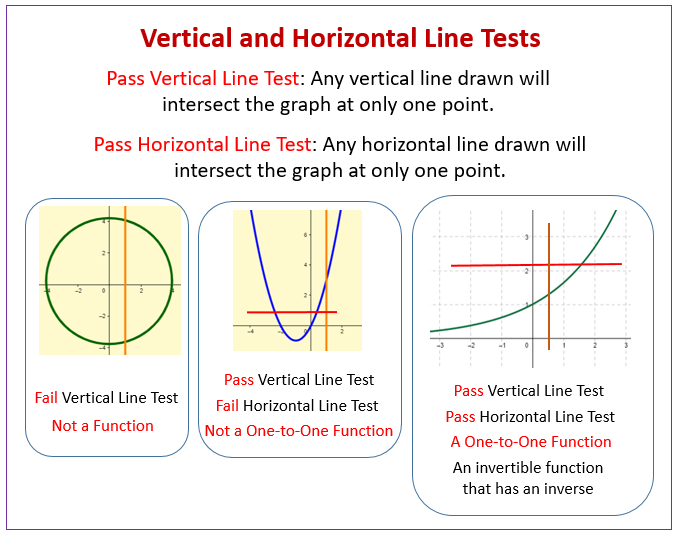
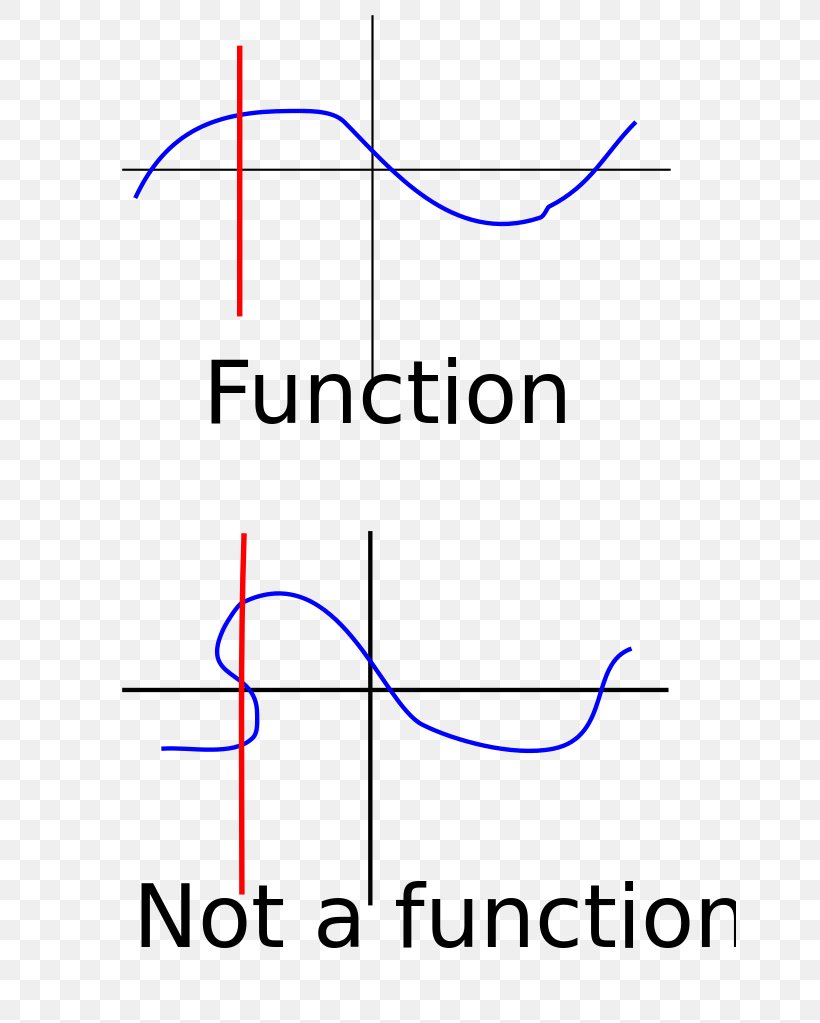
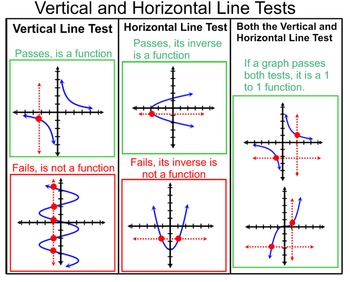
X y 2. The horizontal line test lets you know if a certain function has an inverse function and if that inverse is. The horizontal line test is a convenient method that can determine whether a given function has an inverse but more importantly to find out if the inverse is also a function. Graphs that pass the vertical line test are graphs of functions.

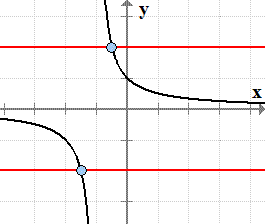
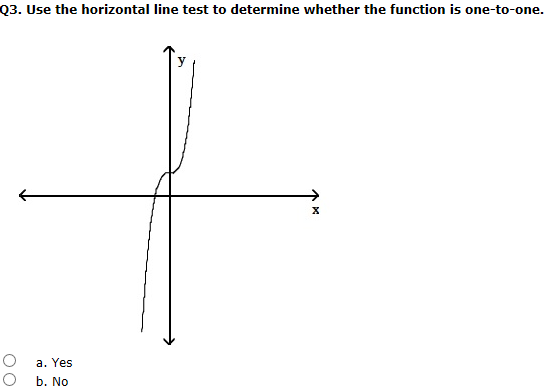
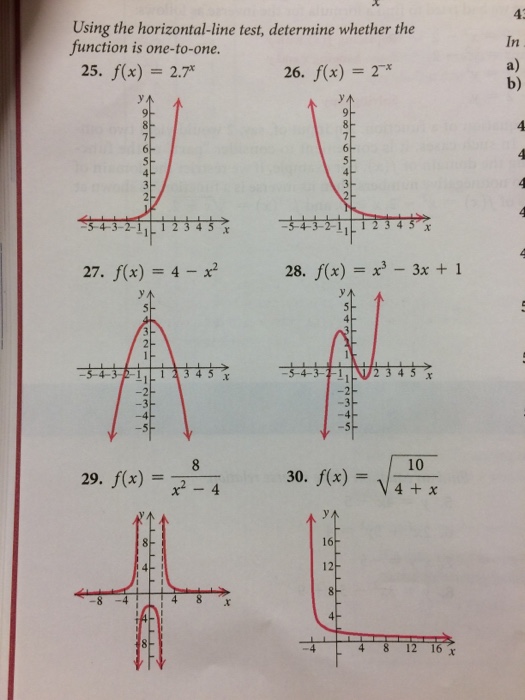
It is called the. What s known as the horizontal line test is an effective way to determine if a function has an inverse function or not. Identify a function with the horizontal line test all functions pass the vertical line test but only one to one functions pass the horizontal line test. Otherwise it has no inverse function.

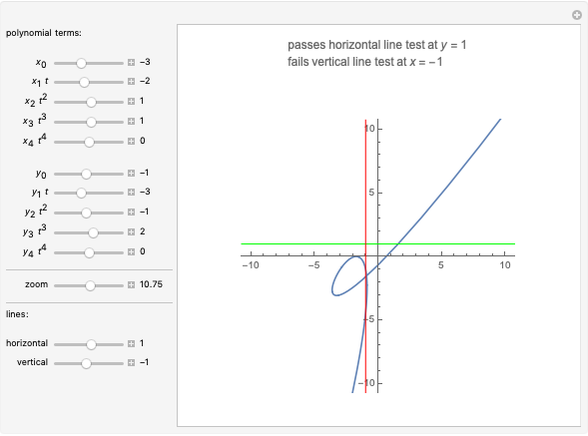
Variations of the horizontal line test can be used to determine whether a function is surjective or bijective. This method is called the horizontal line test. F is bijective if and only if any horizontal line will intersect the graph. The horizontal line test tells you if a function is one to one.

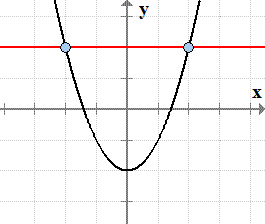
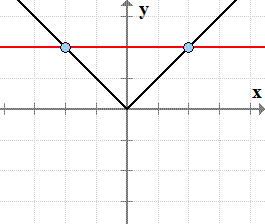
Remember that it is very possible that a function may have an inverse but at the same time the inverse is not a function because it doesn t pass the vertical line test. It is used exclusively on functions that have been graphed on the coordinate plane. The function y f x is a function if it passes the vertical line test. If a horizontal line intersects a function s graph more than once then the function is not one to one.

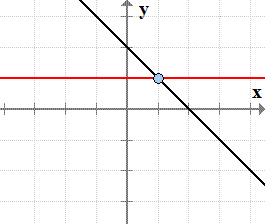
It is a one to one function if it passes both the vertical line test and the horizontal line test. If no two different points in a graph have the same second coordinate this means that horizontal lines cross the graph at most once. A test use to determine if a function is one to one. If the horizontal line touches the graph only once then the function does have an inverse function.